Définition
\(\triangleright\) Définition d'un oscillateur amorti
Un oscillateur amorti est un oscillateur dont la force de rappel ne dépend plus linéairement de l'élongation.
Pour ce type d'oscillateur, la Loi de Hooke n'est plus valable
Formalisme mathématique
\(\triangleright\) Equation du mouvement d'un oscillateur amorti
L'oscillateur amorti évolue selon l'équation:
$${{\ddot x+2\gamma\dot x+\omega_0^2x=0}}$$
Avec:- \(2\gamma= {{\frac{\lambda}{m} }}\): taux d'amortissement (\(s^{-1})\)
- \(\lambda\): coefficient de frottement
- \(\omega_0= \sqrt\frac{k}{m}\): la pulsation propre
- \(k\): la constante de raideur
- \(m\): la masse du mobile en mouvement
:
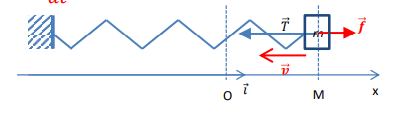
Retrouver l'équation du mouvement de l'oscillateur amorti
1
On applique le
Deuxième loi de Newton - Principe fondamental de la dynamique en considérant le frottement: \(\vec f=-\lambda\frac{d\vec{OM} }{dt}\)
2
On a alors en projettant selon \(\vec i\):
$$m\ddot x +\lambda \dot x+kx=0$$
On pose:
\(\omega_0=\sqrt\frac{k}{m}\)
\(2\gamma=\frac\lambda m\)
3
Finalement, on a:
$$\ddot x+2\gamma\dot x+\omega_0^2x=0$$
\(\triangleright\) Solution de l'équation du mouvement d'un oscillateur armonique
La solution générale de l'équation est de la forme
$$x(t)={{Ae^{r_1t}+Be^{r_2t} }}$$
Avec:
\(r_1\) et \(r_2\): les racines de l'équation \(r^2+2\gamma r+\omega_0^2=0\)
Facteur de qualité
Oscillateurs - Facteur de qualité
On peut réécrire le discrimant avec le facteur de qualité: \(\Delta= {{-4\omega_0^2(1-\frac{1}{4Q^2})}}\)
Différents régimes
Oscillateurs - Régime pseudo-périodique
\(\triangleright\) Equation horaire en régime pseudo-périodique
$$x(t)={{C.e^{-\gamma t}\cos(\omega_p t+\phi)}}$$
Avec:- \(\omega_p=\left (\omega_0\sqrt{1-\frac 1{4Q^2} }\right)\): la pseudo-période
- \(\gamma\): taux d'amortissement
Oscillateurs - Régime apériodique
\(\triangleright\) Equation horaire en régime apériodique
$$x(t)={{e^{-\gamma t}\left (C.\cosh(\omega_a t+\phi)+D.\sinh(\omega_a t)\right)}}$$
Avec:- \(\omega_a=\left (\omega_0\sqrt{\frac 1{4Q^2} - 1}\right)\): la pseudo-période
- \(\gamma\): taux d'amortissement
Oscillateurs - Régime critique
\(\triangleright\) Equation horaire en régime critique
$$x(t)={{e^{-\gamma t} \left( A+Bt\right)}}$$- \(\gamma\): taux d'amortissement
Représentation dans l'espace des phases
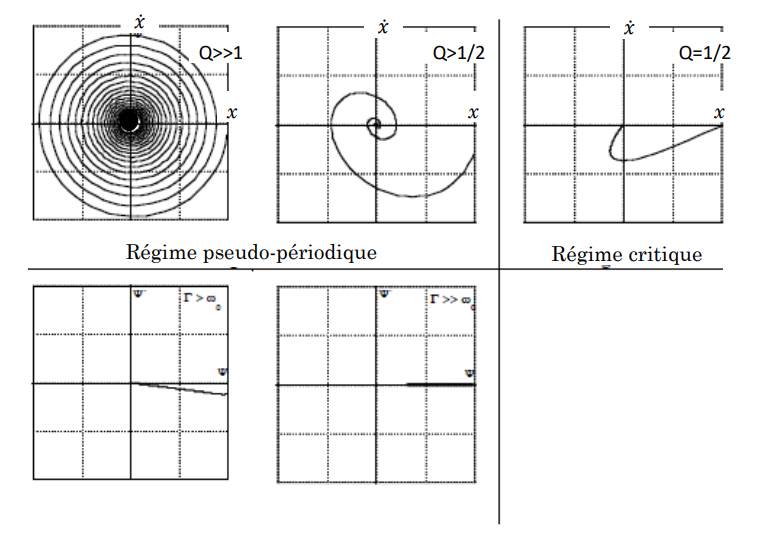
Aspect énergétique
\(\triangleright\) Expression de l'énergie mécanique d'un oscillateur amorti en régime pseudo-périodique
Pour ce cas, on regarde un oscillateur avec un facteur de qualité (Oscillateurs - Facteur de qualité) \(Q\gt \gt 1\). Donc, la pseudo-période dévient très rapidement la période propre.
Pour un oscillateur amorti, l'énergie mécanique diminue avec le temps:
$$E_m\approx {{\frac 12 k C^2e^{-2\gamma t} }}$$
Avec:- \(\gamma\): taux d'amortisement

